Երկրաչափություն

                                                        Հարթաչափություն
Կան եռանկյան մի քանի տեսակներ՝ ոււղանկյուն եռանկյուն,կամայական եռանկյուն,հավասարասրույն եռանկյուն,հավասարակողմ եռանկյուն։
Ուղանկյուն եռանկյուն՝

Ուղանկյուն եռանկյունը է այն եռանկյուն  որի 1 անկյունը հավասար է 90*։

c ներքնաձիքն է

 a և b էջերն են;

Բանաձևեր ուղղանկյուն եռանկյան մասին

a^2+b^2=c^2

h^2=ac*bc             a^2=acc

S=ab/2              b^2=bcc

h=ab/c

S=hc/2

                                                                 Հավասարասրույն եռանկյուն

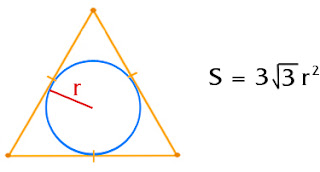
Հավասարակողմ եռանկյուն են անվանում այն եռանկյան որի բոլոր կողմերը հավասր են և բոլոր անկյունները հավասար են 60  աստիճանի։

                                                                 

                               Տարածաչափություն

Մի ուղղի վրա չգտնվող ցանկացած երեք կետով անցնում է հարթություն, այն էլ

միայն մեկը:

Եթե ուղղի երկու կետերը գտնվում են հարթության մեջ, ապա ուղիղը պատ- կանում է այդ հարթությանը:

Եթե երկու հարթություն ունեն ընդհանուր կետ, ապա նրանք ունեն այդ կետով անցնող ընդհանուր ուղիղ, որի վրա գտնվում են այդ հարթությունների բոլոր ընդհանուր կետերը:

Ուղղով և նրա վրա չգտնվող կետով անցնում է հարթություն, այն էլ միայն մեկը:

Երկու հատվող ուղղով անցնում է հարթություն, այն էլ միայն մեկը:

Խորանարդ

Sհ=a^2

Sկ=4a^2

Sլ=6a^2

V=a^3

Գլան

 

V = π R² h

Sհ=πR^2

Sկ=2πRh

Sլ=2πRh+2π^2R

Կոն

V = 1/3πR^2հ

Sհ=π^2R

Sկ=πRl

Sլ=πRl+π^2R

Գունդ

V = 4/3πR^3

S=4πR^2

Լոգարիթմական ֆունկցիաներ

Լոգարիթմական ֆունկցիաներ

           Լոգարիթմական ֆունկցիա կոչվում է F(X)=logax   բանաձևով  տրված ֆունկցիան, որտեղ a-ն մեկից տարբեր դրական թիվ է ։

1)Ֆունկցիայի որոշման տիրույթն ամբողջ թվային առանցքն է D(F)=(0.)

2)Ֆունկցիայի արժեքների բազմությոնն է դրական կիսաառանցքը՝ E(F)=(-,)

3)ֆունկցիան մոնոտոն է իր որոշման տիրույթում։Ընդ որում,այն որում,այն աճող է եթե a>1 և նվազող՝ եթե  0<a<1։

4)Ֆունկցիան 0 արժեք ընդունում է x =1

5) ա) a>1 դեպքում ֆունկցիան բացասական է  (0,1) և դրական՝ (1,)  միջակայքում,

     բ)0<a<1 դեպում ֆունկցիան դրական է (0,1) և բացասական՝   (1,) միջակայքում։

Օրինակ՝

F(X)=X+ln(-X)

Գտնել ֆունկցիայի որոշման տիրույթը։

D(F)=(-** ;0)

Գտնել ֆունկցիայի կրիտիկական կետերը։

F`(X)=1+1/X

(X+1)/X=0

X=-1

Գտնել ֆունկցիայի մեծագույն արժեքը [-4;-0.5] հատվածում;

F(-4)=-4+ln4

F(-1)=-1+0=-1

F(-0.5)=-0.5+ln0.5

Ցուցչային ֆունկցիա

Ցուցչային ֆունկցիա կոչվում է F(X)=a^X բանաձևով տրված ֆունկցիան է, որտեղ a-ն 1 տարբեր որևէ թիվ է։

1)Ֆունկցիայի որոշման տիրույթն ամբողջ թվային առանցքն է D(F)=R

2) Ֆունկցիան դրական է ամբողջ թվային առանցքի վրա։

3)Ֆունկցիան մոնոտոն է ամբողջ թվային առանցքի վրա ընդ որում այն արճող է, եթե a>1 նվազող է 0<a<1

4)Ֆունկցիան սահմանափակ է ներքևից զրո թվով և սահմանափակ չէ վերևից։

5)Ֆունկցիայի արժեքների բազմությոնն է դրական կիսաառանցքը՝ E(F)=(0,)

Օրինակ՝

Y=e^2x

Գտնել ֆունկցիայի արժեքը X=ln5

Y=e^2ln5=25

Գտնել ֆունկցիայի որոշման տիրույթը։

D(F)=R

Գտնելy(x) ֆունկցիայի գրաֆիկին նրա X₀=0 աբցիս ունեցող կետում տարված շոշափողի հավասարումը:

Y=0(0-X)+1=1

Աստիճանային ֆունկցիա

    Աստիճանային ֆունկցիա

Եթե a կենտ է։

Աստիճանային ֆունկցիա կոչվում է F(X)=X^a բանաձևով տրված ֆունկցիան է, որտեղ a-ն զրոյից տարբեր որևէ թիվ է։

1)Ֆունկցիայի որոշման տիրույթն ամբողջ թվային առանցքն է D(F)=R

2) Ֆունկցիան կենտ է

3)Ֆունկցիան ունի մեկ զրո F(0)=0

4)Ֆունկցիան դրական է, երբ X և բացասական ՝ երբ X

5)Ֆունկցիան աճում է ամբողջ թվային առանցքը վրա։

6)Ֆունկցիայի արժեքների բազմությունն ամբողջ թվային առանցքն է ՝E(F)=R,ֆունկցիան անսահմանափակ է և չունի մեծագույն ու փոքրագույն արժեքներ։

եթե a զույգ է

1)Ֆունկցիայի որոշման տիրույթն ամբողջ թվային առանցքն է D(F)=R

2) Ֆունկցիան զույգ է

3)Ֆունկցիան ունի մեկ զրո F(0)=0

4)Ֆունկցիան դրական է, երբ X հավասար չէ 0

5)Ֆունկցիան նվազում է X և աճում է X

6)Ֆունկցիայի արժեքների բազմությունն ամբողջ թվային առանցքն է ՝E(F)= ,ֆունկցիան անսահմանափակ է և չունի մեծագույն ու փոքրագույն արժեքներ։

Օրինակ՝ F(X)=X^2-X

ԳտնելF ֆունկցիայի ածանցյալը X=2 կետում։

F`(X)=2X-1

F(2)=2*2-1=3

ԳտնելF ֆունկցիայի մեծագույն արժեքը [-1;1]

ԳտնելF ֆունկցիայի ֆունկցիայի փոքրագույն արժեքը։

2X-1=0  X=0.5

F(0.5)=-0.25.   F(-1)=0.  F(1)=0

ԳտնելF ֆունկցիայի կրտիկական կետերը։

2X-1=0

X=0.5

Կոորդինատային մեթոդ և վեկտորներ

A(X₁;Y₁) և B(X₂;Y₂)  ծայրակետերով AB հատվածի միջնակետի կոորդինատ-ները որոշվում են հետևյալ բանաձևերով. X=( X₁+ Y₁)/2 ,Y=(Y₁ + Y₂)/2

  A(X₁;Y₁) և B(X₂;Y₂)   ծայրակետերով AB հատվածի  d_ab երկարությունը հավասար է` d_ab=  

O(X₀;Y₀) կենտրոնով և R շառավղով շրջանագծի հավասարումն է (X- X₀)^2+(Y- Y₀)^2=r^2

Հատվածը, որի համար նշված է սկիզբն ու վերջը, կոչվում է ուղղորդված հատված կամ վեկտոր:

Վեկտորը, որի սկիզբն ու վերջը համընկնում են, կոչվում է զրոյական վեկտոր

Համագիծ վեկտորներ են կոչվում այն ոչ զրոյական վեկտորները, որոնք գտնվում են կամ նույն ուղղի, կամ զուգահեռ ուղիղների վրա: Զրոյական վեկտորը համարվում է համագիծ ցանկացած վեկտորի: Ոչ համագիծ վեկտորները կոչվում են տարագիծ վեկտորներ:

Համուղղված վեկտորներ են կոչվում այն համագիծ վեկտորները, որոնց սկզբնա- կետերը զուգահեռ տեղափոխությամբ համընկեցնելիս ծայրակետերը գտնվում են սկզբնակետի միևնույն կողմում:

Հակուղղված վեկտորներ են կոչվում այն համագիծ վեկտորները, որոնց սկզբնա- կետերը զուգահեռ տեղափոխությամբ համընկեցնելիս ծայրակետերը գտնվում են սկզբնակետի տարբեր կողմում:

Ցանկացած a  , b  և c  վեկտորների համար տեղի ունեն հետևյալ հավասարություն- ները:

                           Վարժությունների լուծումներ

1․Տրված են A(-1;3),B(3;1),O(0;0)

Գտնել BA վեկտորի կորդինատները

BA{-4;2}

Գտնել AB հատվածի միջնակետի կորդինատները։

(1;2)

Գտնել AB վեկտորի երկարությունը։

AB= =5

Գտնել AO և ՕB վեկտորների կազմած անկյան աստիճանային չափը։

cosB=(X₁+X₂+Y₁+Y₂)/ |AO|*|OB|=0/|AO|*|OB|=0

B=90